Question

The standard form of the equation of a circle is (x−5)2+(y−6)2=1. What is the general form of the equation?

x2+y2+10x+12y+60=0
x2+y2−10x−12y−62=0
x2+y2+10x+12y+62=0
x2+y2−10x−12y+60=0

Answer 1

The answer is x2+y2−10x−12y+60=0. Hope this helps!✌

Answer 2

x2+y2−10x−12y+60=0

Explanation:

The standard form of the equation of a circle is usually given in the form;

`(x-a)^(2) +(y-b)^(2)=r^(2)`

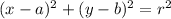
The center of the circle is (a, b) while r denotes the radius.

The general form of the equation of a circle is obtained by expanding the brackets, collecting like terms and simplifying.

The standard form in this case has been given as;

(x−5)^2+(y−6)^2=1

We simply open the brackets and simplify to obtain the general form;

(x−5)^2 = (x−5) (x−5)

= x^2 -5x -5x +25

= x^2 -10x +25

(y−6)^2 = (y-6) (y-6)

= y^2 -6y - 6y +36

= y^2 -12y +36

(x−5)^2+(y−6)^2 = x^2 -10x +25 + y^2 -12y +36 = 1

x^2 -10x +25 + y^2 -12y +36 = 1

x^2 + y^2 -10x -12y +25 + 36 = 1

x^2 + y^2 -10x -12y + 60 = 0