Answer:
C. 0
Explanation:
The points of intercection between the graph of a quadratic function of the form
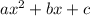 are given by the discriminant of the quadratic formula.
are given by the discriminant of the quadratic formula.
Remember that the quadratic formula is:
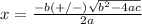
The discriminant of he quadratic formula is just the thing inside the radical, in other words:
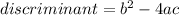
- If the discriminant is negative, the graph of the quadratic function doesn't intercept the x-axis.
- If the discriminant is positive, the graph of the quadratic function intercept the x-axis at 2 points.
- If the discriminant is 0, the graph of the quadratic function intercept the x-axis at 1 point.
We can infer form our quadratic that
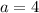 ,
,
 , and
, and
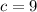 , so let's replace the values in the discriminant:
, so let's replace the values in the discriminant:
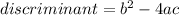
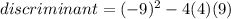
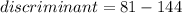
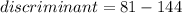
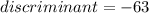
Since the discriminant is negative, we can conclude that the graph of the quadratic function doesn't intercept the x-axis at any point.