Question

At how many points does the graph of function below intercept the

x axis y=4x^2-9x+9?

A.2
B.1
C.0

Answer 1

c

Explanation:

0

Answer 2

C. 0

Explanation:

The points of intercection between the graph of a quadratic function of the form
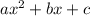`ax^(2) +bx+c` are given by the discriminant of the quadratic formula.

Remember that the quadratic formula is:

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac } }{2a}`

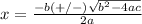
The discriminant of he quadratic formula is just the thing inside the radical, in other words:

`discriminant=b^(2) -4ac`

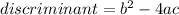
- If the discriminant is negative, the graph of the quadratic function doesn't intercept the x-axis.

- If the discriminant is positive, the graph of the quadratic function intercept the x-axis at 2 points.

- If the discriminant is 0, the graph of the quadratic function intercept the x-axis at 1 point.

We can infer form our quadratic that
`a=4`,
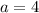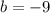`b=-9`, and
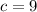`c=9`, so let's replace the values in the discriminant:

`discriminant=b^(2) -4ac`

`discriminant=(-9)^(2) -4(4)(9)`

`discriminant=81-144`

`discriminant=81-144`

`discriminant=-63`

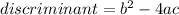
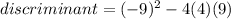
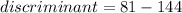
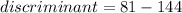
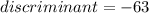
Since the discriminant is negative, we can conclude that the graph of the quadratic function doesn't intercept the x-axis at any point.