Question

in the 1980s, an average mortgage range was around 18.75%. how much less per month would a $125,000 30 year mortgage be today if the current rate were 5%?

Answer 1

The current per month mortgages are $1289.54 less than the earlier per month mortgages.

Explanation:

The EMI formula is =
`(p* r* (1+r)^(n) )/((1+r)^(n)-1 )`

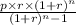
Here p = 125000

For case 1:

r = 18.75/12/100=0.015625

n =
`30*12=360`

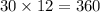
So, putting values in formula we get :

`(125000* 0.015625* (1+0.015625)^(360) )/((1+0.015625)^(360)-1 )`

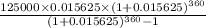
= $1960.51

For case 2:

r = 5/12/100=0.004166

n =
`30*12=360`

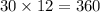
So, putting values in formula we get :

`(125000* 0.004166* (1+0.004166)^(360) )/((1+0.004166)^(360)-1 )`

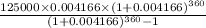
= $670.97

Now we will find the difference between both EMI's

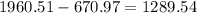`1960.51-670.97=1289.54` dollars.

Therefore, the current per month mortgages are $1289.54 less than the earlier per month mortgages.

Answer 2

$1289.48

Explanation:

A financial calculator tells you the payment with the higher interest rate is $1960.51, and that with the lower interest rate is $671.03. The difference in payment amounts is ...

$1960.51 -671.03 = $1289.48