Double angle (or half angle, depending how you look at it) identities:
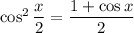
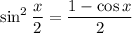
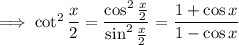
So we have
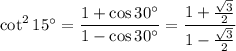
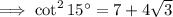
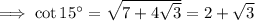
Note that when taking the square root, we should take into account that that could yield two possible solutions, but we know
 and
and
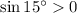 , so it's also the case that
, so it's also the case that
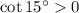 .
.
Also, the reason we have equality in the last step can be explained like so:
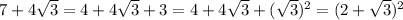
(not unlike the process used to complete the square)