Question

Find the exact value of cot(15degrees) using half angle formulas?

Answer 1

C

Explanation:

C on edg

Answer 2

Double angle (or half angle, depending how you look at it) identities:

`\cos^2\frac x2=\frac{1+\cos x}2`

`\sin^2\frac x2=\frac{1-\cos x}2`

`\implies\cot^2\frac x2=(\cos^2\frac x2)/(\sin^2\frac x2)=(1+\cos x)/(1-\cos x)`

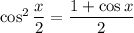
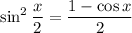
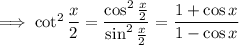
So we have

`\cot^215^\circ=(1+\cos30^\circ)/(1-\cos30^\circ)=\frac{1+\frac{\sqrt3}2}{1-\frac{\sqrt3}2}`

`\implies\cot^215^\circ=7+4\sqrt3`

`\implies\cot15^\circ=√(7+4\sqrt3)=2+\sqrt3`

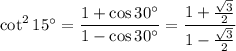
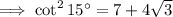
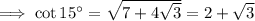
Note that when taking the square root, we should take into account that that could yield two possible solutions, but we know
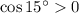`\cos15^\circ>0` and
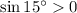`\sin15^\circ>0`, so it's also the case that
`\cot15^\circ>0`.

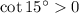Also, the reason we have equality in the last step can be explained like so:

`7+4\sqrt3=4+4\sqrt3+3=4+4\sqrt3+(\sqrt3)^2=(2+\sqrt3)^2`

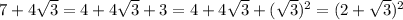
(not unlike the process used to complete the square)