Answer:
The length of the kite string in terms of trigonometric ratios, if we call it L, is
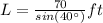
Explanation:
As we have to use the trigonometric ratios, and knowing that in a right triangle the relation
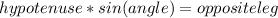
is valid. We call the hypotenuse as L, and we know the other two data (angle and opposite leg), so we have that
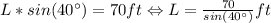
Then,
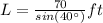
is the answer that we are looking for to solve the problem.