Question

Express the length of the kite string in terms of trigonometric ratios. A) 70cos40° B) 70sin40° C) 40 sin70° D) 70 sin40°

Answer 1

D

Explanation:

just took it

70 over sin40 degrees

Answer 2

The length of the kite string in terms of trigonometric ratios, if we call it L, is
`L=(70)/(sin(40\°))ft`

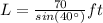
Explanation:

As we have to use the trigonometric ratios, and knowing that in a right triangle the relation

`hypotenuse*sin(angle)=opposite leg`

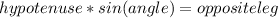
is valid. We call the hypotenuse as L, and we know the other two data (angle and opposite leg), so we have that

`L*sin(40\°)=70ft\Leftrightarrow L=(70)/(sin(40\°))ft`

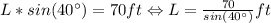
Then,

`L=(70)/(sin(40\°))ft`

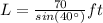
is the answer that we are looking for to solve the problem.