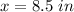Answer:
x = 8.5in, y = 17in, r = 28°, s = 62°
Explanation:
If ΔJNZ and ΔKOA are similar, then corresponding sides are in proportion and corresponding angles are congruent.
We have the proportion:
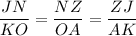
and equations:
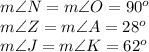
We have:
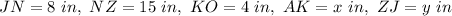
For y we must use the Pythagorean theorem:
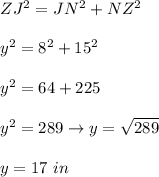
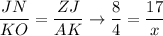 cross multiply
cross multiply
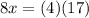
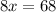 divide both sides by 8
divide both sides by 8