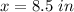2 Answers

Luis Dalmolin · Answer 1 · 2020-08-16T23:20:17+0000

Answer:

x = 8.5in, y = 17in, r = 28°, s = 62°

Explanation:

If ΔJNZ and ΔKOA are similar, then corresponding sides are in proportion and corresponding angles are congruent.

We have the proportion:

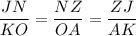
(JN)/(KO)=(NZ)/(OA)=(ZJ)/(AK)

and equations:

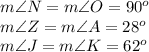
$m\angle N=m\angle O=90^o\\m\angle Z=m\angle A=28^o\\m\angle J=m\angle K=62^o$

We have:

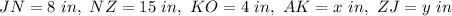
$JN=8\ in,\ NZ=15\ in,\ KO=4\ in,\ AK=x\ in,\ ZJ=y\ in$

For y we must use the Pythagorean theorem:

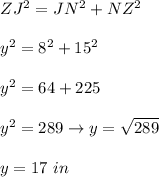
$ZJ^2=JN^2+NZ^2\\\\y^2=8^2+15^2\\\\y^2=64+225\\\\y^2=289\to y=√(289)\\\\y=17\ in$

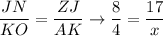$(JN)/(KO)=(ZJ)/(AK)\to(8)/(4)=(17)/(x)$ cross multiply

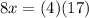
8x=(4)(17)

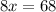8x=68 divide both sides by 8

$x=8.5\ in$