Question

Which statement about g(x)=x^2-576 is true

a. the zeros, -288 and 288, can be found when 0=(x+288)(x-288.
b. the only zero,288 , can be found when 0=(x-288)^2.
c. the zeros, -24 and 24, can be found when 0= (x+24)(x-24).
d. the only zero, 24, can be found when 0=(x-24)^2

Answer 1

The zeros, -24 and 24, can be found when 0= (x+24)(x-24).

Explanation:

Answer 2

c. the zeros, -24 and 24, can be found when 0= (x+24)(x-24).

Explanation:

The given function is

`g(x)=x^2-576`

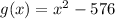
When we equate the function to zero, we obtai;

`x^2-576=0`

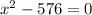
Use difference of two squares:

`x^2-24^2=0`

`(x-24)(x+24)=0`

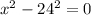
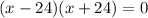
Use the zero product property to obtain;

`x-24=0,\:and\:x+24=0`

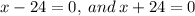
This implies that;

`x=24,\:and\:x=-24`

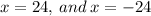
The correct choice is C