Answer:
c. the zeros, -24 and 24, can be found when 0= (x+24)(x-24).
Explanation:
The given function is
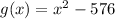
When we equate the function to zero, we obtai;
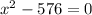
Use difference of two squares:
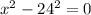
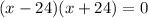
Use the zero product property to obtain;
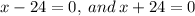
This implies that;
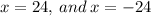
The correct choice is C