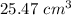Question

A sphere of radius 2.3 cm fits exactly in a cylinder with the same radius. Complete the steps to determine the volume of space in the cylinder that is not being taken up by the sphere. Calculate the volume of the cylinder to the nearest tenth. V = cm3 Calculate the volume of the sphere to the nearest tenth. V = cm3 Determine the of the volumes to find the leftover space. The volume of space in the cylinder that is not being taken up by the sphere is about cm3.

Answer 1

Part 1) The volume of the cylinder is
`76.41\ cm^(3)`

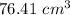
Part 2) The volume of the sphere is
`50.94\ cm^(3)`

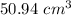
Part 3) Determine the difference of the volumes to find the leftover space

Part 4) The volume of space in the cylinder that is not being taken up by the sphere is about
`25.47\ cm^(3)`

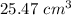
Explanation:

step 1

Calculate the volume of the cylinder

`V=\pi r^(2)h`

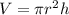
we have

`r=2.3\ cm`

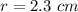
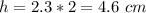`h=2.3*2=4.6\ cm` -----> the height is the diameter of the sphere

substitute the values

`V=(3.14)(2.3)^(2)(4.6)=76.41\ cm^(3)`

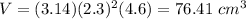
step 2

Calculate the volume of the sphere

`V=(4)/(3)\pi r^(3)`

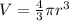
we have

`r=2.3\ cm`

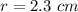
substitute the values

`V=(4)/(3)(3.14)(2.3)^(3)=50.94\ cm^(3)`

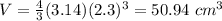
step 3

Determine the difference of the volumes to find the leftover space

`76.41\ cm^(3)-50.94\ cm^(3)=25.47\ cm^(3)`

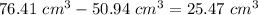
therefore

The volume of space in the cylinder that is not being taken up by the sphere is about
`25.47\ cm^(3)`