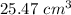Answer:
Part 1) The volume of the cylinder is
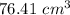
Part 2) The volume of the sphere is
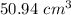
Part 3) Determine the difference of the volumes to find the leftover space
Part 4) The volume of space in the cylinder that is not being taken up by the sphere is about
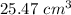
Explanation:
step 1
Calculate the volume of the cylinder
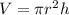
we have
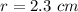
 -----> the height is the diameter of the sphere
-----> the height is the diameter of the sphere
substitute the values
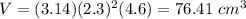
step 2
Calculate the volume of the sphere

we have
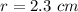
substitute the values
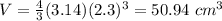
step 3
Determine the difference of the volumes to find the leftover space
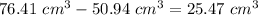
therefore
The volume of space in the cylinder that is not being taken up by the sphere is about