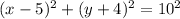Question

Type the correct answer in each box.

A circle is centered at the point (5, -4) and passes through the point (-3, 2).
The equation of this circle is (x + ___)^2 + (y + ___)^2 = ___.

Answer 1

Answer:
`(x-5)^2+(y+4)^2=10^2`

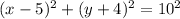
Explanation:

The standard of equation of a circumference has the form:

`(x-a)^2+(y-b)^2=r^2`

Where the point (a,b) is the center of the circumference and r is the radius.

You know the center of the circumference: (5,-4).

Substitute this point into the equation of the circumference:

a=5 and b=-4

Then:

`(x-5)^2+(y+4)^2=r^2`

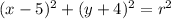
Now you need to find the radius. Substitute the point (-3,2) into the circumference and solve for r:

`(-3-5)^2+(2+4)^2=r^2\\(-8)^2+(6)^2=r^2\\64+36=r^2\\r=√(100)\\r=10`

The equation of this circumference is:

`(x-5)^2+(y+4)^2=10^2`

Answer 2

`(x-5)^2+(y+4)^2=100`

Or type

(x + _-5__)^2 + (y + _4__)^2 = _100__.

Explanation:

First find the radius of the circle using the distance formula;

`r=√((x_2-x_1)^2+(y_2-y_1)^2)`

Substitute the points to get;

`r=√((5--3)^2+(-4-2)^2)`

`r=√(8^2+(-6)^2)`

`r=√(64+36)`

`r=√(100)`

r=10 units

We now substitute the center (h,k)=(5,-4) and r=10 into the standard equation of the circle;

`(x-h)^2+(y-k)^2=r^2`

`(x-5)^2+(y--4)^2=10^2`

`(x-5)^2+(y+4)^2=100`