Answer:
The set of solutions will change
Observe the image attached
Explanation:
We have the following compound inequality
 and
and
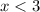
This can be written as:
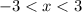
The expression "and" in this context means that the values of x must be greater than -3 and at the same time they must be less than 3.
Then the set of solution is given by the intersection of both inequalities: the interval (-3, 3)
If we change the expression "and" by the expression "or" then it is no longer necessary for both inequalities to be fulfilled at the same time. That is, x will be greater than -3 or less than 3. The set of solutions will be the union of both inequalities.
Therefore the set of solutions will change and it will be
x ∈ (-∞, 3) U (-3, ∞)
x ∈ (-∞, ∞)