Question

Does changing the compound inequality x > −3 and x < 3 from “and” to “or” change the solution set? Explain

Answer 1

The set of solutions will change

Observe the image attached

Explanation:

We have the following compound inequality
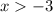`x> -3` and
`x <3`

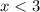
This can be written as:

`-3 <x <3`

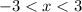
The expression "and" in this context means that the values of x must be greater than -3 and at the same time they must be less than 3.

Then the set of solution is given by the intersection of both inequalities: the interval (-3, 3)

If we change the expression "and" by the expression "or" then it is no longer necessary for both inequalities to be fulfilled at the same time. That is, x will be greater than -3 or less than 3. The set of solutions will be the union of both inequalities.

Therefore the set of solutions will change and it will be

x ∈ (-∞, 3) U (-3, ∞)

x ∈ (-∞, ∞)

Answer 2

Yes, if you change the type of compound inequality, the solution set will change. The solution set of the “and” compound inequality contains values for x that satisfy both inequalities, which are values between –3 and 3. The solution set of the “or” compound inequality contains values for x that satisfy either or both inequalities, which includes all real numbers.

Explanation:

sample response given from edge