Answer:
206.35 square units.
Explanation:
We have been given a triangular pyramid. We are asked to find total surface area of our given pyramid.
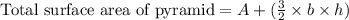 , where,
, where,
A = Area of base of pyramid,
b = Base of one of faces,
h = Height of one of faces.
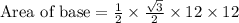
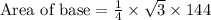
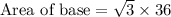
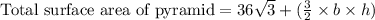
We know that height of an isosceles triangle is
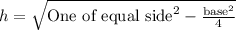 .
.
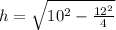

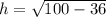
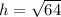
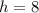
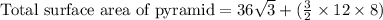


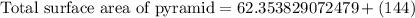
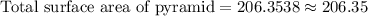
Therefore, the total surface area of our given pyramid is 206.35 square units.