Question

Find the total area for the regular pyramid.

Answer 1

206.35 square units.

Explanation:

We have been given a triangular pyramid. We are asked to find total surface area of our given pyramid.

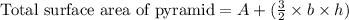`\text{Total surface area of pyramid}=A+((3)/(2)* b* h)`, where,

A = Area of base of pyramid,

b = Base of one of faces,

h = Height of one of faces.

`\text{Area of base}=(1)/(2)* (√(3))/(2)* 12* 12`

`\text{Area of base}=(1)/(4)* √(3)* 144`

`\text{Area of base}=√(3)* 36`

`\text{Total surface area of pyramid}=36√(3)+((3)/(2)* b* h)`

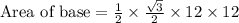
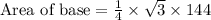
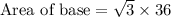
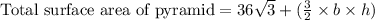
We know that height of an isosceles triangle is
`h=\sqrt{\text{One of equal side}^2-\frac{\text{base}^2}{4}}`.

`h=\sqrt{10^2-(12^2)/(4)}`

`h=\sqrt{100-(144)/(4)}`

`h=√(100-36)`

`h=√(64)`

`h=8`

`\text{Total surface area of pyramid}=36√(3)+((3)/(2)* 12* 8)`

`\text{Total surface area of pyramid}=36√(3)+(3* 48)`

`\text{Total surface area of pyramid}=36√(3)+(144)`

`\text{Total surface area of pyramid}=62.353829072479+(144)`

`\text{Total surface area of pyramid}=206.3538\approx 206.35`

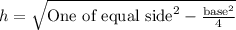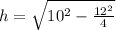
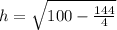
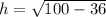
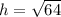
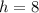
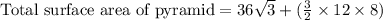
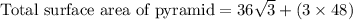
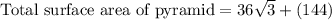
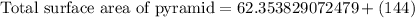
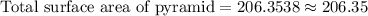
Therefore, the total surface area of our given pyramid is 206.35 square units.