Question

If you know the centripetal force acting on an object moving in a circle, which equation will allow you to calculate the velocity of the object

Answer 1

A, sqrt(Fr/m)

Step-by-step explanation:

We know that force is equal to mass times acceleration. Centriptial acceleration is v^2/r. Therefore:

`F= m*a\\a = (v^2)/(r)\\ F= m*(v^2)/(r)\\(F*r)/(m)= v^2\\ v= \sqrt{(F*r)/(m)}`

That's how I got A.

Answer 2

The velocity of the object in circular motion,
`v=\sqrt{(F_cr)/(m)}`

Step-by-step explanation:

The second law of motion given the magnitude of force acting on an object. It is equal to the product of its mass and acceleration i.e.

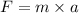`F=m* a`..........(1)

In a circular path the acceleration of the object is called centripetal acceleration,
`a=(v^2)/(r)`

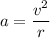
Equation (1) becomes,

`F=m* (v^2)/(r)`

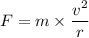
We know that, in circular motion the force acting on the object is centripetal force. The formula for centripetal force is given by :

`F_c=m* (v^2)/(r)`

`v=\sqrt{(F_cr)/(m)}`

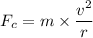
So, the correct option is (a). Hence, this is the required solution.