Answer:
1. Vertex: (3,4)
2. It opens down.
3. The y-intercept is -5
Explanation:
1. For a quadratic function in the form
 , you can calculate the x-coordinate of the vertex with:
, you can calculate the x-coordinate of the vertex with:
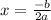
Then, given the function
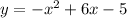 , you can identify that:
, you can identify that:
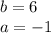
Substituting, you get:
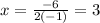
Substitute
 into
into
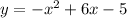 to find the y-coordinate of the vertex:
to find the y-coordinate of the vertex:
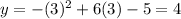
Then the vertex is at (3,4)
2. You identified above the value of "a". This is:

Then, since
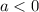 , the parabola opens down.
, the parabola opens down.
3. Substitute
 into the function and solve for "y":
into the function and solve for "y":
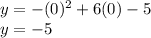
Therefore, the y-intercept is -5