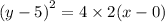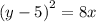Question

What is the equation of a parabola whose vertex is (0, 5) and whose directrix is x = 2?

A.
y2 = 8(x − 5)

B.
8(y − 5) = x2

C.
(y − 5)2 = 8x

D.
(y − 5)2 = -8x

Answer 1

Answer: D. (y − 5)2 = -8x

Step-by-step explanation: I got this correct on Edmentum.

Answer 2

C.

`{(y - 5)}^(2) = 8x`

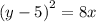
Step-by-step explanation

It was given that, the vertex of the parabola is (0,5).

The directrix of this parabola is x=2.

The directrix tells us that, the parabola will open horizontally in the positive x-axis direction.

Hence the equation of this parabola is of the form;

`{(y - k)}^(2) = 4p(x - h)`

we plug in the vertex h=0, k=5 to get,

`{(y - 5)}^(2) = 4p(x - 0)`

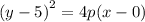
p is the distance from the vertex to the directrix, which is

`p = 2 - 0 = 2`

Hence, we the equation of the parabola becomes,

`{(y - 5)}^(2) = 4 * 2(x - 0)`

`{(y - 5)}^(2) = 8x`