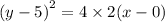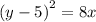ANSWER
C.
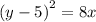
Step-by-step explanation
It was given that, the vertex of the parabola is (0,5).
The directrix of this parabola is x=2.
The directrix tells us that, the parabola will open horizontally in the positive x-axis direction.
Hence the equation of this parabola is of the form;
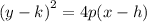
we plug in the vertex h=0, k=5 to get,
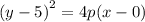
p is the distance from the vertex to the directrix, which is
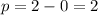
Hence, we the equation of the parabola becomes,