Question

Solve for x by using log. Rounded to hundredth.


`4^(2x-5) =6^(-x+1)`

Answer 1

x = 1.91

Explanation:

* We have exponential equation to solve it lets study some rules

- If a^m = a^n ⇒ then m = n

- If a^m = b^m ⇒ then a = b or m = 0

- If a^m = b^n ⇒ log(a^m) = log(b^n) ⇒ m log(a) = n log(b)

* You can use log or ln

* Lets solve the problem

∵
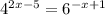`4^(2x-5)=6^(-x+1)` ⇒ insert log to both sides

∴
`log(4^(2x-5))=log(6^(-x+1))`

-
`log(a^(m))=mlog(a)`

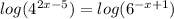
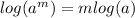
∴ (2x - 5)log(4) = (-x + 1)log(6) ⇒ open the brackets

∴ 2xlog(4) - 5log(4) = -xlog(6) + log(6) ⇒ collect x in one side

∴ 2xlog(4) + xlog(6) = log(6) + 5log(4) ⇒ take x as a common factor

∴ x(2log(4) + log(6)) = log(6) + 5log(4)

- divide both sides by coefficient of x

`x=(log(6)+5log(4))/(2log(4)+log(6))=1.91`

∴ x = 1.91

Answer 2

Answer:
`x=1.91`

Explanation:

Given the expression
`4^(2x-5) =6^(-x+1)`, apply logarithm to both sides. Then:

`log(4)^(2x-5) =log(6)^(-x+1)`

Remembert that according the the properties of logarithms:

`log(a)^n=nlog(a)`

Then:

`(2x-5)log(4)=(-x+1)log(6)`

Appy distributive property and solve for "x":

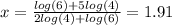
`2xlog(4)-5log(4)=-xlog(6)+log(6)\\2xlog(4)+xlog(6)=log(6)+5log(4)\\x(2log(4)+log(6))=log(6)+5log(4)\\\\x=(log(6)+5log(4))/(2log(4)+log(6))\\\\x=1.91`