Question

A single die is rolled twice. The set of 36 equally likely outcomes is {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6),}. Find the probability of getting two numbers whose sum is less than 13.

Answer 1

its (3,6) i think so

Answer 2

Answer: 1 (certain)

Explanation:

Given : A single die is rolled twice.

The set of 36 equally likely outcomes is

{(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6),}.

We can see that the maximum sum of two numbers on dice is 12 .

So the number of pairs that make sum less than 13 = 36

Now, the probability of getting two numbers whose sum is less than 13 will be :-

`=(36)/(36)=1`

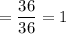
Hence, the probability of getting two numbers whose sum is less than 13 is 1 ( certain event)