Question

HELP PLEASE! Can you please explain so I can understand how it was completed?

Determine two pairs of polar coordinates for the point (3, -3) with 0°≤ θ < 360°. (1 point)

(3 square root of 2 , 315°), (-3 square root of 2 , 135°)

(3 square root of 2 , 225°), (-3 square root of 2 , 45°)

(3 square root of 2 , 45°), (-3 square root of 2 , 225°)

(3 square root of 2 , 135°), (-3 square root of 2 , 315°)

Answer 1

(3 square root of 2 , 135°), (-3 square root of 2 , 315°)

Explanation:

Hello!

We need to determine two pairs of polar coordinates for the point (3, -3) with 0°≤ θ < 360°.

We know that the polar coordinate system is a two-dimensional coordinate. The two dimensions are:

• The radial coordinate which is often denoted by r.

• The angular coordinate by θ.

So we need to find r and θ. So we know that:

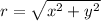`r=\sqrt{x^(2)+y^(2)}` (1)

x = rcos(θ) (2)

x = rsin(θ) (3)

From the statement we know that (x, y) = (3, -3).

Using the equation (1) we find that:

`r=\sqrt{x^(2)+y^(2)}=\sqrt{3^(2)+(-3)^(2)} = 3√(2)`

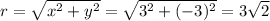
Using the equations (2) and (3) we find that:

3 = rcos(θ)

-3 = rsin(θ)

Solving the system of equations:

θ= -45

Then:

r = 3\sqrt{2}[/tex]

θ= -45 or 315

Notice that there are two feasible angles, they both have a tangent of -1. The X will take the positive value, and Y the negative one.

So, the solution is:

(3 square root of 2 , 135°), (-3 square root of 2 , 315°)