How do you solve this question? Differentiate: x √(x) - {x}^(2) √(x) ​

Question

How do you solve this question? Differentiate:


`x √(x) - {x}^(2) √(x)`
​

Answer 1

`\displaystyle (d)/(dx)[x√(x)-x^(2)√(x)]`

`\displaystyle =(3)/(2)√(x) - (5)/(2)\;x√(x)`

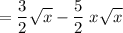
Explanation:

There's no need for the product rule. Consider the following:

• 
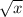  `√(x)` is the same as
  `x^(1/2)`

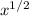
As a result,

• 
  `x√(x) = x\cdot x^(1/2) = x^(3/2)`, and
• 
  `x^(2)√(x) = x^(2)\cdot x^(1/2) = x^(5/2)`.

`\displaystyle x√(x)-x^(2)√(x) = x^(3/2) - x^(5/2)`.

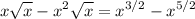How to differentiate the first term,
`x^(3/2)`?

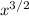Apply the power rule.

`\displaystyle (d)/(dx) [x^(3/2)] = \underbrace{3/2}_{\begin{aligned}&\text{from}\\[-0.5em]& \text{power}\end{aligned}} \;x^((3/2) - 1) = (3)/(2)\;x^(1/2)`.

`\displaystyle (d)/(dx) [x^(5/2)] = \underbrace{5/2}_{\begin{aligned}&\text{from}\\[-0.5em]& \text{power}\end{aligned}} \;x^((5/2) - 1) = (5)/(2)\;x^(3/2)`.

The derivative of difference is the difference of derivatives. Rewrite
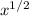`x^(1/2)` back as
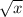`√(x)` since the question uses square roots rather than fraction power.

`\displaystyle\begin{aligned} (d)/(dx)[x√(x)-x^(2)√(x)] &=(d)/(dx)[x√(x)] - (d)/(dx)[x^(2)√(x)] \\&=(3)/(2)\;x^(1/2) - (5)/(2)\;x^(3/2)\\ &=(3)/(2) √(x) - (5)/(2) x√(x)\end{aligned}`.