Question

Select the point that is a solution to the system of inequalities

Answer 1

The correct answer option is C. (2, 6).

Explanation:

We are given the following inequalities so we will check each point if it satisfies them:

`y<x^2+6`

`y>x^2-4`

A. (0, 8):

`y<x^2+6` --->
`8<0^2+6 = 8<6` - False

`y>x^2-4` --->
`8>0^2-4 = 8 > -4` - True

B. (4, 2):

`y<x^2+6` --->
`2<4^2+6 = 2<22` - True

`y>x^2-4` --->
`2>4^2-4 = 2> 12` - False

C. (2, 6):

`y<x^2+6` --->
`6<2^2+6 = 6<10` - True

`y>x^2-4` --->
`6>2^2-4 = 6> 0` - True

D. (-2, -4):

`y<x^2+6` --->
`-4<(-2)^2+6 = -4<10` - True

`y>x^2-4` --->
`-4>(-2)^2-4 = -4> 0` - False

Therefore, the point which is the solution to this system of inequalities is C. (2, 6).

Answer 2

Hello!

The answer is:

The point C. (2,6) is a solution to the system of inequalities.

Why?

To check what point is a solution to the system of inequalities, the point must satisfy both inequalities, so:

We are given the inequalities:

`y<x^(2)+6\\y>x^(2)-4`

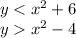
Checking, we have:

- Substituting A(0,8), we have:

First inequality,

`y<x^(2)+6\\8<0^(2)+6\\8<6`

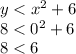
Now, since 8 is not less than 6, we know that A (0,8) is not a solution to the system of inequalities since it does not satisfy both inequalities.

- Substituting B(4,2), we have:

First inequality,

`y<x^(2)+6\\2<4^(2)+6\\2<16+6\\2<22`

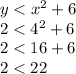
Second inequality,

`y>x^(2)-4\\2>4^(2)-4\\2>16-4\\2>12`

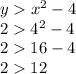
Now, since 2 is not greater than 12, we know that B(4,2) is not a solution to the system of inequalities since it does not satisfy both inequalities.

- Substituting C(2,6), we have:

First inequality,

`y<x^(2)+6\\6<2^(2)+6\\6<4+6\\6<10`

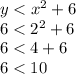
Second inequality,

`y>x^(2)-4\\6>2^(2)-4\\6>4-4\\6>0`

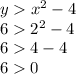
Now, as we can se, both inequalities are satisfied since 6 is less than 10 and greater than 0, so C(2,6) is a solution to the system.

- Substituting D(-2,-4)

`y<x^(2)+6\\-4<-2^(2)+6\\-4<4+6\\-4<10`

Second inequality,

`y>x^(2)-4\\-4>2^(2)-4\\-4>4-4\\-4>0`

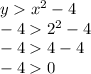
Now, since -4 is not greater than 0, we know that D(-2,-4) is not a solution to the system of inequalities since it does not satisfy both inequalities.

Hence,

Only the point C. (2,6) is a solution to the system of inequalities.

Have a nice day!