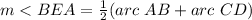Answer:
The measure of angle BEA is
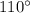
Explanation:
we know that
The measure of the inner angle is the semi-sum of the arcs comprising it and its opposite
so
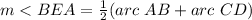
step 1
Find the measure of arc AD
Remember that the inscribed angle is half that of the arc it comprises.
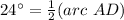
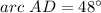
step 2
Find the measure of arc BC
Remember that the inscribed angle is half that of the arc it comprises.
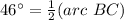
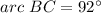
step 3
Find the measure of (arc AB + arc CD)
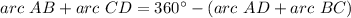
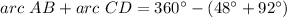
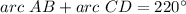
step 4
Find the measure of angle BEA