Answer: Third quartile =$21.58
Explanation:
Let x be value of a stock .
For uniform distribution,
probability density function =
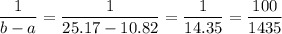
Let a be the stock value such that P(x<a) =75% or 0.75
![\Rightarrow\ \int ^(a)_(10.82)f(x)\ dx=0.75\\\\\Rightarrow\ \int ^(a)_(10.82)(100)/(1435)\ dx=0.75\\\\\Rightarrow(100)/(1435)[x]^(a)_(10.82)=0.75\\\\\Rightarrow (100)/(1435)(a-10.82)=0.75\\\\\Rightarrow a-10.82=0.75*(1435)/(100)\\\\\Rightarrow a-10.82=10.7625\\\\\Rightarrow a= 10.7625+10.82= $$21.5825\approx $$21.58](https://img.qammunity.org/2022/formulas/mathematics/college/o6au69ei9bawjrfjn280664wbgr5vwf5ye.png)
Hence, 75% of all days the stock is below $21.58 or Third quartile =$21.58 .