Hello!
The answer is:
The correct option is D.
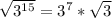
Why?
To solve this problem, we must remember the following properties:
Product of powers with the same base:
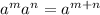
Power of a power:
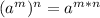
Also, we must remember that if we want to introduce a number into a root, in order to not change the expression, we need to introduce it with the same exponent:
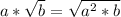
So, solving the problem, we have:
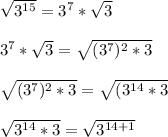

Hence,
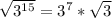
So, the correct option is D.
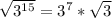
Have a nice day!