Question

Please help me on this

Answer 1

The answer is D because the square root of 3^15 is 2187 square root of 3. Now if you add 3^7 then that gives you 2187. So your answer would be D

Answer 2

Hello!

The answer is:

The correct option is D.
`\sqrt{3^(15) }=3^(7)* √(3)`

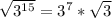
Why?

To solve this problem, we must remember the following properties:

Product of powers with the same base:

`a^(m)a^(n)=a^(m+n)`

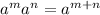
Power of a power:

`(a^(m))^(n)=a^(m*n)`

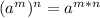
Also, we must remember that if we want to introduce a number into a root, in order to not change the expression, we need to introduce it with the same exponent:

`a*√(b)=\sqrt{a^(2)*b }`

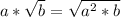
So, solving the problem, we have:

`\sqrt{3^(15) }=3^(7)*√(3)\\\\3^(7)*√(3)=\sqrt{(3^(7))^(2) *3}\\\\\sqrt{(3^(7))^(2) *3}=\sqrt{(3^(14) *3}\\\\\sqrt{3^(14) *3}=\sqrt{3^(14+1)`

`\sqrt{3^(14+1) } =\sqrt{3^(15)}`

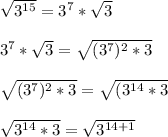
Hence,

`\sqrt{3^(15) }=3^(7)* √(3)`

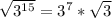
So, the correct option is D.
`\sqrt{3^(15) }=3^(7)* √(3)`

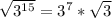
Have a nice day!