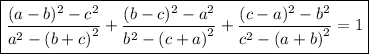Plz help with full process \frac{(a - b)^(2) - {c}^(2) }{{a}^(2) - {(b+ c)}^(2) } + \frac{(b - c)^(2) - {a}^(2) }{{b}^(2) - {(c+ a)}^(2) } + \frac{(c - a)^(2) - {b}^(2) }{{c}^(2…

Question

Plz help with full process


`\frac{(a - b)^(2) - {c}^(2) }{{a}^(2) - {(b+ c)}^(2) } + \frac{(b - c)^(2) - {a}^(2) }{{b}^(2) - {(c+ a)}^(2) } + \frac{(c - a)^(2) - {b}^(2) }{{c}^(2) - {(a+ b)}^(2) }`
​

Answer 1

Siblings r annoying

Explanation:

Answer 2

`\displaystyle \frac{(a - b)^(2) - {c}^(2) }{{a}^(2) - {(b+ c)}^(2) } + \frac{(b - c)^(2) - {a}^(2) }{{b}^(2) - {(c+ a)}^(2) } + \frac{(c - a)^(2) - {b}^(2) }{{c}^(2) - {(a+ b)}^(2) }=1`

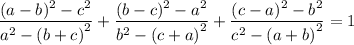
Explanation:

Algebra Simplifying

We are given the expression:

`\displaystyle T=\frac{(a - b)^(2) - {c}^(2) }{{a}^(2) - {(b+ c)}^(2) } + \frac{(b - c)^(2) - {a}^(2) }{{b}^(2) - {(c+ a)}^(2) } + \frac{(c - a)^(2) - {b}^(2) }{{c}^(2) - {(a+ b)}^(2) }`

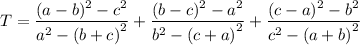
We need to repeatedly use the following identity:

`(a^2-b^2)=(a-b)(a+b)`

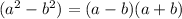
For example, the first numerator has a difference of squares thus we factor as:

`(a - b)^(2) - {c}^(2) =(a-b-c)(a-b+c)`

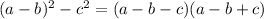
The first denominator can be factored also:

`{a}^(2) - {(b+ c)}^(2) = (a-b-c)(a+b+c)`

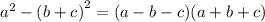
Applying the same procedure to all the expressions:

`\displaystyle T=((a - b- c)(a-b+c) )/(a-b-c)(a+b+c) ) + ((b - c - a)(b-c+a) )/((b-c-a)(b+c+a) ) + ((c - a-b)(c-a+b) )/((c-a-b)(c+a+b))`

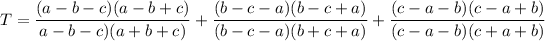
Simplifying all the fractions:

`\displaystyle T=(a - b- c)/(a+b+c) + (b-c+a)/(b+c+a ) + (c-a+b )/(c+a+b)`

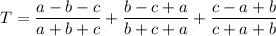
Since all the denominators are equal:

`\displaystyle T=(a - b+ c+b-c+a+c-a+b)/(a+b+c)`

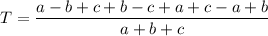
Simplifying:

`\displaystyle T=(a +c+b)/(a+b+c)`

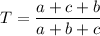
Simplifying again:

T = 1

Thus:

`\boxed{\displaystyle \frac{(a - b)^(2) - {c}^(2) }{{a}^(2) - {(b+ c)}^(2) } + \frac{(b - c)^(2) - {a}^(2) }{{b}^(2) - {(c+ a)}^(2) } + \frac{(c - a)^(2) - {b}^(2) }{{c}^(2) - {(a+ b)}^(2) }=1}`