The equation of the circumference of a circle in terms of
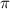 is
is
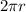 or
or
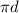 .
.
The circumference for a circle with diameter 10 is
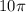 .
.
The circumference for a circle with diameter 19 is
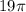 .
.
The circumference for a circle with diameter 30 is
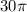 .
.
The circumference for a circle with diameter 16 is
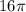 .
.
Relatively easy, right?
The equation of the area of a circle in terms of
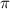 is
is
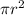 .
.
The area of a circle with radius 5 is
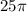 .
.
The area of a circle with radius 9.5 is
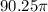 .
.
The area of a circle with radius 15 is
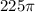 .
.
The area of a circle with radius 8 is
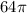 .
.
Hope this helped!
(By the way, I don't know why you're using hard formulas for trying to find the radius or diameter. The diameter is simply twice the radius, and the radius is simply half the diameter.)