Hello!
The answer is: The resultant force is equal to 200 lb.
Why?
From the statement, we know that both forces are acting at right angles, meaning that there is a vertical force and a horizontal force.
We can solve this problem using the Pythagorean Theorem, which states that:
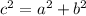
Let be:
a, the horizontal force (x)
b, the vertical force (y)
c, the resultant force (r)
So, assuming that:
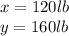
Calculating the resultant force, we have:
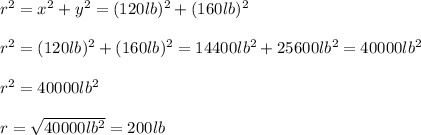
Hence, the resultant force is equal to 200 lb.
Have a nice day!