Question

What are the dimensions of the product?

Answer 1

2 x 2

Explanation:

Dimensions: m x n

m = number of rows

n = number of columns

When multiplying two matrices:

m x n * n x k = m x k

MATIX 1:

m = number of rows

n = number of columns

MATRIX 2:

n = number of rows

k = number of columns

RESULTING MATIX:

m = number of rows

k = number of columns

2 x 3 * 3 x 2 = 2 x 2

Answer 2

The correct option is 2.

Explanation:

The given matrix multiplication is

`\begin{bmatrix}2&4&-3\\ 6&1&0\end{bmatrix}* \begin{bmatrix}-3&2\\ -2&3\\ -8&5\end{bmatrix}`

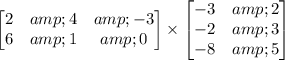
Order of matrix = Number of rows × Number of columns

Let
`A=\begin{bmatrix}2&4&-3\\ 6&1&0\end{bmatrix},B=\begin{bmatrix}-3&2\\ -2&3\\ -8&5\end{bmatrix}`

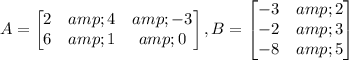
Order of matrix A = 2 × 3

Order of matrix B = 3 × 2

The order of product of two matrices is

`A_(m* n)\cdot B_(n* k)=AB_(m* k)`

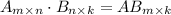
It means

Order of product = Number of rows of first matrix × Number of columns of second matrix

Order of product = 2 × 2

`A_(2* 3)\cdot B_(3* 2)=AB_(2* 2)`

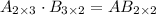
The dimensions of the product are 2 × 2. Therefore the correct option is 2.