Question

The initial temperature of the water in a constant-pressure calorimeter is 24°C. A reaction takes place in the calorimeter, and the temperature rises to 87°C. The calorimeter contains 367 g of water, which has a specific heat of 4.18 J/(g·°C). Calculate the enthalpy change (ΔH) during this reaction

Answer 1

Step-by-step explanation:

For a chemical reaction, the enthalpy of reaction (ΔHrxn) is … ... to increase the temperature of 1 g of a substance by 1°C; its units are thus J/(g•°C). ... Both Equations 12.3.7 and 12.3.8 are under constant pressure (which ... The specific heat of water is 4.184 J/g °C (Table 12.3.1), so to heat 1 g of water by 1 ..

Answer 2

Answer : The enthalpy change during the reaction is 4.74 kJ/mole

Explanation :

First we have to calculate the heat released during the reaction.

`q=m* c* (T_(final)-T_(initial))`

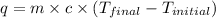
where,

q = heat released = ?

`c` = specific heat of water =
`4.18J/g^oC`

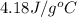
m = mass of water = 367 g

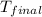`T_(final)` = final temperature of water =
`87^oC`

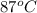
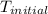`T_(initial)` = initial temperature of metal =
`24^oC`

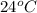
Now put all the given values in the above formula, we get:

`q=367g* 4.18J/g^oC* (87-24)^oC`

`q=96645.78J=96.6kJ`

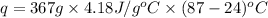
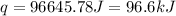
Thus, the heat released during the reaction = 96.6 kJ

Now we have to calculate the enthalpy change during the reaction.

`\Delta H=(q)/(n)`

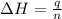
where,

`\Delta H` = enthalpy change = ?

q = heat released = 96.6 kJ

n = number of moles water =
`\frac{\text{Mass of water}}{\text{Molar mass of water}}=(367g)/(18g/mol)=20.4mole`

`\Delta H=(96.6kJ)/(20.4mole)=4.74kJ/mole`

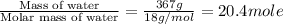
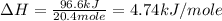
Therefore, the enthalpy change during the reaction is 4.74 kJ/mole