Answer:
W = 2 cm
L = 5 cm
Explanation:
A rectangle is a four sided shape with 4 perpendicular angles. It has two pairs of parallel sides which are equal in distance: width and length. Its area, the amount of space inside it, can be found using the formula A = l*w. If the area is 10 cm² and the length is "3 cm less than 4 times the width" or 4w - 3, you can substitute and solve for w.
A = l*w
10 = (4w - 3)(w)
10 = 4w² - 3w
Subtract 10 from both sides to make the equation equal to 0. Then solve the quadratic by quadratic formula.
4w² - 3w - 10 = 0
Substitute a = 4, b = -3 and c = -10.
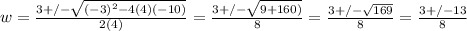
There are two possible solutions which can be found.
3 + 13 / 8 = 16/ 8 = 2
3 - 13 / 8 = -10/8 = -5/4
Since w is a side length or distance, it must be positive so w = 2 cm.
If the width is 2 cm then the length is 4(2) - 3 = 8 - 3 = 5 cm.