ANSWER
The solution of the system shown is (2k,k)
EXPLANATION
The given system of equations are:
First equation:
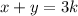
Second equation:
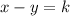
We consider this to be a simulation equation in x and y, and then treat k as a constant.
Let us eliminate y, by adding the two equations:
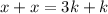
This implies that:
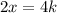
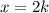
Let us now substitute x=2k into any of the equations, say , the second equation.

Group similar terms.
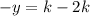
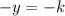
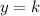
The solution is therefore (2k,k)
The last choice is correct.