Question

Which table represents a linear function?

Answer 1

Third Option

Explanation:

We know that a function is linear if its slope or "rate of change" remains constant throughout the domain of the function.

A linear equation has the following formula:

`y = mx + b` where m is the constant rate of change.

So if
`y = f (x)`

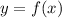
For any x value, it is always true that:

`f(x + 1) - f (x) = m`

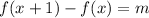
Notice that among the options given the only table where this is fulfilled is in the third table

`f (1 + 1) - f (1) = m\\f (2) -f (1) = m\\-5 - (- 3) = -2 = m\\`

`f (3) -f (2) = m\\-7 - (- 5) = -2 = m`

`f (4) - f (3) = m\\-9 - (- 7) = -2 = m`

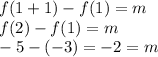
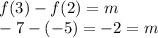
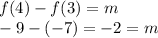
m is constant. Therefore the function is linear

Answer 2

ANSWER

Third table

EXPLANATION

The table that represents a linear function has a constant difference in both the x-values and the y-values.

The x-values are having a constant difference of 1 for all the tables.

First table.

Difference in y: 12-6≠6-3

Second Table

Difference in y: 9-5≠5-2

Third table

Difference in y:


`- 5 - - 3 = - 7 - - 5 = - 9 - - 7 = - 2`

Fourth table.

Different in y:-4--2≠-2--4

Hence the third table is the correct choice.