Question

Radioactive​ uranium-235 has a​ half-life of about 700 million years. Suppose you find a rock and chemical analysis tells you that only one sixteenth

of the​ rock's original​ uranium-235 remains. How old is the​ rock?

A.
2.8 billion years old

B.
1.4 billion years old

C.
175 million years old

D.
2.1 billion years old

E.
3.5 billion years old

F.
350 million years old

Answer 1

Option A.

Explanation:

Half life of Uranium-235 has been given as 700 million years.

Since radioactive decay is an exponential phenomenon so the formula will be

`A_(t)=A_(0)e^(-kt)`

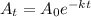
where
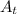`A_(t)` = Amount of the radioactive element at the time 't'

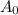`A_(0)` = Initial amount

t = time for decay

k = decay constant

By this formula,

`(A_(0))/(2)=A_(0)e^(-kt)`

`(1)/(2)=e^{-700* 10^(6) k}`

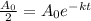
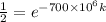
By taking natural log on both the sides,

`ln((1)/(2))=ln(e^{-700* 10^(6)k } )`

`-ln2=-700* 10^(6)* k`

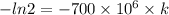
0.693147 =
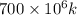
`700* 10^(6)k`

k =
`(0.693147)/(700* 10^(6))`

=
`(0.693147)/(7* 10^(8))`

=
`9.9* 10^(-10)`

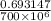
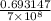
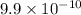
Now we have to find the age of the rock which is one sixteenth of the original rock.

By the formula again,

`A_(t)=A_(0)e^(-kt)`

`(A_(0))/(16)=A_(0)e^(-kt)`

`(1)/(16)=e^{-9.9* 10^(-10)t}`

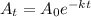
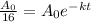
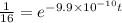
Taking log on both the sides.

`ln(1)/(16)=ln(e^{-9.9* 10^(-10)t})`

`2.772588=-9.9* 10^(-10)* t`

t =
`(2.772588)/(9.9* 10^(-10) )`

t =
`0.28* 10^(10)`

t =
`2.8* 10^(9)`

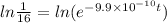
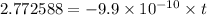
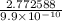
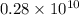
Therefore, the rock is 2.8 billion years old.

Option A. is the answer.

Answer 2

A. 2.8 billion years old

Explanation:

1/16 = (1/2)^4, so 4 half-lives have elapsed.

4 · 0.700 billion years = 2.8 billion years

The rock is 2.8 billion years old.