Answer:
Option A.
Explanation:
Half life of Uranium-235 has been given as 700 million years.
Since radioactive decay is an exponential phenomenon so the formula will be
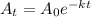
where
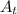 = Amount of the radioactive element at the time 't'
= Amount of the radioactive element at the time 't'
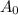 = Initial amount
= Initial amount
t = time for decay
k = decay constant
By this formula,
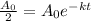
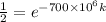
By taking natural log on both the sides,
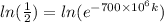
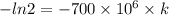
0.693147 =
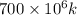
k =
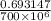
=
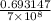
=
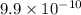
Now we have to find the age of the rock which is one sixteenth of the original rock.
By the formula again,
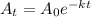
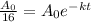
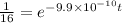
Taking log on both the sides.
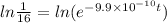
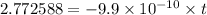
t =
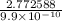
t =
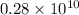
t =

Therefore, the rock is 2.8 billion years old.
Option A. is the answer.