Answer: The correct option is (A) 11.
Step-by-step explanation: Given the following table that shows the function f :
x 2 3 4 5 6
f(x) ? 15 23 39 71
We are to determine the value of f(2) that will lead to an average rate of change of 15 over the interval [2, 6].
We know that
the rate of change of a function g(x) over an interval [a, b] is given by
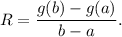
From the table, we note that
f(6) = 71 and f(2) = ?
So, the rate of change of the function f(x) over the interval [2, 6] is given by
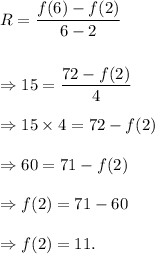
Thus, the required value of f(2) is 11.
Option (A) is CORRECT.