Answer:
Second option 3; -3
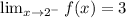
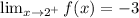
Explanation:
We want to find:
 and
and
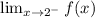
When x tends to 2 on the left then
 .
.
When x is less than 2
 . This implies that the limit of f(x) when x approaches 2 from the left is equal to 3. Observe the attached image.
. This implies that the limit of f(x) when x approaches 2 from the left is equal to 3. Observe the attached image.
This is:
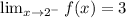
Also When x tends to 2 on the rigtn then
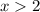 .
.
When x is greater than 2
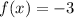 . This implies that the limit of f(x) when x approaches 2 from the rigth is equal to -3. This is:
. This implies that the limit of f(x) when x approaches 2 from the rigth is equal to -3. This is:
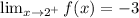 Observe the attached image.
Observe the attached image.