Answer:
The probability of obtaining a score less than 60 is 2.28%
It happens 2 out of 100 times.
Explanation:
If the mean μ = 80 and the standard deviation σ = 10, then we need to find the probability that an X value is less than 60.
Then we find
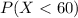
To find this probability we use the Z statistic.
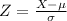
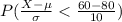
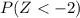
This is the same as
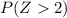
We look for this value in the table for the normal distribution of right queue and we have:
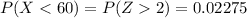
The probability of obtaining a score less than 60 is 2.28%
It happens 2 out of 100 times.