Question

I’m another normally distributed test score is 80 and the standard deviations is 10. How common are values in the less than 60? Show your work

Answer 1

The probability of obtaining a score less than 60 is 2.28%

It happens 2 out of 100 times.

Explanation:

If the mean μ = 80 and the standard deviation σ = 10, then we need to find the probability that an X value is less than 60.

Then we find

`P(X <60)`

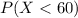
To find this probability we use the Z statistic.

`Z = (X- \mu)/(\sigma)`

`P((X- \mu)/(\sigma)<(60-80)/(10))`

`P(Z <-2)`

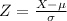
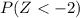
This is the same as

`P(Z> 2)`

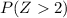
We look for this value in the table for the normal distribution of right queue and we have:

`P(X <60) = P(Z> 2) = 0.02275`

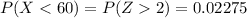
The probability of obtaining a score less than 60 is 2.28%

It happens 2 out of 100 times.