Which statement about y = x2 − x3 is true? a.It is not a function. b.It is an even function. c.It is neither an odd nor an even function. d.It is an odd function.

Question

asked Dec 11, 2020 21.8k views

2 Answers

Andrew Ferrier · Answer 1 · 2020-12-13T23:41:33+0000

Answer:

Option c. It is neither an odd nor an even function.

Explanation:

The equation
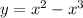y = x^2 - x^3 is a function, because there is a single value of y for each value of the domain x.

To test if it is an even function we must do
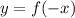y = f(-x) . If
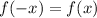f(-x) = f(x) then it is an even function.

If
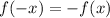f(-x) = -f(x) then it is an odd function

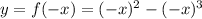
y = f(-x) = (-x) ^ 2 - (- x) ^ 3

Simplifying we have:

y = x ^ 2 + x ^ 3

f(-x) is not equal to f(x) so the function is not even.

f(-x) is not equal to -f(x) so the function is not odd.

THE correct answer is the option c

Vss · Answer 2 · 2020-12-16T17:13:02+0000

ANSWER

c.It is neither an odd nor an even function.

EXPLANATION

The given function is

$y = f(x) = {x}^(2) - {x}^(3)$

If this function is odd, then f(-a)=-f(a).

$f( - a) = {( - a)}^(2) - {( - a)}^(3)$

$f( - a) = {( a)}^(2) + {( a)}^(3)$

Now ,

$f( a) = {( a)}^(2) - {( a)}^(3)$

$- f( a) = - {( a)}^(2) + {( a)}^(3)$

Since

$f( - a) \\e - f(a)$

The function is not odd.

Also if the function is even, then

f( a) = f( - a)

Since

$f( a) \\e f( - a)$

the function is not even.

Hence the function is neither even nor odd.