Question

The function f(x)=2^x and g(x)=f(x+k). If k= -5, what can be concluded about the graph of g(x)?

The graph of g(x) is shifted vertically
a. 5 units above the graph of f(x)
b. 5 units below the graph of f(x)
c. the graph is not shifted vertically from the graph of f(x)

The graph of g(x) is shifted horizontally
a. 5 units to the left of the graph of f(x)
b. 5 units to the right of the graph of f(x)
c. the graph is not shifted horizontally from the graph of f(x)

Answer 1

Answer: The graph of g(x) is shifted vertically- c.

The graph of g(x) is shifted horizontally- b.

Step-by-step explanation: if k is positive then the function moves to the the left. If k is negative the function is shifted to the right.

Answer 2

The graph of g(x) is shifted horizontally 5 units to the right of the graph of f(x).

Explanation:

Given :The function f(x)=
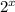`2^(x)` and g(x)=f(x+k). If k= -5,

To find : what can be concluded about the graph of g(x).

Solution : The function parent f(x) =
`2^(x)` .

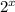By the Transformation rule if f(x) transformed to f(x+k) it would shifted horizontally toward left by k units .

Then ,

g(x)=f(x+ (-5)) would be b. 5 units to the right of the graph of f(x).

Therefore, The graph of g(x) is shifted horizontally 5 units to the right of the graph of f(x).