Question

At Maximum speed, an airplane travels 1680 miles against the wind in 5 hours. Flying with the wind, the plane can Travel the same distance in 4 hours.

Let x be the Maximum speed of the airplane and y be the speed of the wind. what is the speed of the plane with no wind?

Answer 1

x = 378 miles/h

Explanation:

First we calculate the module of both speeds.

With the wind against

`s = (distance)/(time)`

s = d/t

d = 1680 miles

t = 5 hours

s = 1680/5

s = 336 miles/h

`s = x -y` Because the wind speed goes in the direction opposite to that of the plane.

`336 = x -y`

Flying with the wind.

s = 1680/4

s = 420

`s = x + y` Because the wind speed goes in the same direction as the speed of the plane.

`420 = x + y`

Now we have a system of 2 equations and 2 unknowns. We wish to find the value of x.

`336 = x -y\\420 = x + y`

Resolving we have:

`336 = x -y`

+

`420 = x + y`

-------------------------

`756 = 2x`

x = 756/2

x = 378 miles/h

y = 42 miles/h

Answer 2

378 mph

Explanation:

When the plane travels with the wind:

Distance = 1680 miles

Time = 4 hours

Rate = 1681 / 4 = 420 mph

When the plane travels against the wind:

Distance = 1680 miles

Time = 5 hours

Rate = 1681 / 5 = 336 mph

Given the above information, we can write the equations:

`x+y=420`

`x-y=336`

Adding these equations to get:

`2x=756`

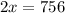
x = 378 mph

Therefore, 378 mph is the speed of the plane in still air.