Answer:
D)
 .
.
Explanation:
All four polynomials are quadratic, meaning that the highest power of the unknown
 in the equation is two.
in the equation is two.
The sign of the quadratic discriminant,
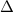 , is a way to tell if a quadratic polynomial comes with non-real solutions.
, is a way to tell if a quadratic polynomial comes with non-real solutions.
There are three cases:
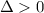 . The quadratic discriminant is positive. There are two real solutions and no non-real solution. The two solutions are different from each other.
. The quadratic discriminant is positive. There are two real solutions and no non-real solution. The two solutions are different from each other.
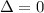 . The quadratic discriminant is zero. There is one real solution and no non-real solution.
. The quadratic discriminant is zero. There is one real solution and no non-real solution.
 . The quadratic discriminant is negative. There is no real solution and two non-real solutions.
. The quadratic discriminant is negative. There is no real solution and two non-real solutions.
How to find the quadratic discriminant?
If the equation is in this form:
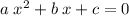 ,
,
where a, b, and c are real numbers (a.k.a. "constants.")
Quadratic discriminant:
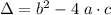 .
.
Polynomial in A:
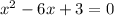 .
.
 .
.
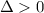 . There will be no non-real solutions and two distinct real solutions.
. There will be no non-real solutions and two distinct real solutions.
Try the steps above for the polynomial in B, C, and D.
- B):
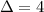 . Two distinct real solutions. No non-real solution.
. Two distinct real solutions. No non-real solution. - C):
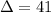 . Two distinct real solutions. No non-real solution.
. Two distinct real solutions. No non-real solution. - D):
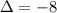 . No real solution. Two distinct non-real solutions.
. No real solution. Two distinct non-real solutions.